Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани — правильные многоугольники. Платоновы тела — трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются «Начала» Евклида.

Доказательство того, что существует ровно пять правильных выпуклых многогранников, очень простое. Рассмотрим развертку вершины такого многогранника. Каждая вершина может принадлежать трем и более граням.

Сначала рассмотрим случай, когда грани многогранника — равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр- многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° — мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° — эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.

Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол 3×90°=270° — получается вершина куба, который также называют гексадром. Добавление еще одного квадрата увеличит угол до 360° — этой развертке уже не соответствует никакой выпуклый многогранник.

Три пятиугольные грани дают угол развертки 3*72°=216 — вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360° — поэтому останавливаемся.

Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.

Таким образом, мы убедились, что существует лишь пять выпуклых правильных многогранников — тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб(гексаэдр)с квадратными гранями и додекаэдр с пятиугольными гранями.

Существует семейство тел, родственных платоновым — это полуправильные выпуклые многогранники, или архимедовы тела. У них все многогранные углы равны, все грани — правильные многоугольники, но нескольких различных типов. Существует 13 или 14 архимедовых тел (число неточное, поскольку псевдоромбокубоктаэдр иногда не причисляют к этому семейству). Кроме того, имеют равные многогранные углы и правильные грани нескольких типов тела из двух бесконечных семейств — призмы и антипризмы (последние также называют скошенными призмами).

Кроме того, платоновым телам близки тела Кеплера-Пуансо, или правильные однородные невыпуклые многогранники.

Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы которых равны, а грани — правильные многоугольники нескольких типов (этим они отличаются от платоновых тел, грани которых — правильные многоугольники одного типа). Открытие тринадцати полуправильных выпуклых многогранников приписывается Архимеду, впервые перечислившего их в не дошедшей до нас работе. Ссылки на эту работу имеются в трудах математика Паппа. Теорией этих тел занимался также Кеплер. Относительно недавно (в конце 50-х — начале 60-х годов XX века) несколько математиков практически одновременно, независимо друг от друга указали на существование еще одного, ранее неизвестного полуправильного выпуклого многогранника -псевдоромбокубоктаэдра Однако не все специалисты согласны с причислением этого многогранника к архимедовым телам.

Множество архимедовых тел можно разбить на несколько групп. Первую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения. Усечением в данном случае называется удаление частей многогранника, расположенных около вершины, вместе с самой вершиной. Для платоновых тел эту процедуру можно провести так, что и получающиеся новые грани, и остающиеся части старых граней будут правильными многоугольниками. Так могут быть получены пять архимедовых тел :усеченный тетраэдр,усеченный куб,усеченный октаэдр, усеченный додекаэдр и усеченный икосаэдр.

Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются кубоктаэдр и икосододекаэдр.

В третью группу входят ромбокубоктаэдр, который иногда называют малым ромбокубоктаэдром и ромбоикосододекаэдр, называемый также малым ромбоикосододекаэдром. Если применить процесс усечения (удаления вершин) к двум квазиправильным телам — кубоктаэдру и икосододекаэдру, то новые полученные грани будут в лучшем случае прямоугольными, однако дальнейшими модификациями их можно преобразовать в квадраты. В эту же группу входят ромбоусеченный кубоктаэдр, иногда называемый большим ромбокубоктаэдром и ромбоусеченный икосододекаэдр, называемый также большим ромбоикосододекаэдром, которые получаются из кубоктаэдра и икосододекаэдра при другом варианте усечения.

В четвертую группу входят две курносые модификации — курносый куб и курносый додекаэдр. Для них характерно несколько повернутое положение граней. В результате эти многогранники, в отличие от предыдущих, не имеют плоскостей симметрии, но имеют оси симметрии. Так как плоскостей симметрии нет, то зеркальное отражение такого тела не совпадает с исходным телом, и поэтому существуют по две формы каждого из них — «правая» и «левая», отличающиеся так же, как правая и левая руки.

Наконец, последняя группа состоит из единственного многогранника — псевдоромбокубоктаэдра, открытого лишь в XX веке. Он может быть получен из ромбокубоктаэдра, если повернуть одну из восьмиугольных чаш на 45°.

К семейству архимедовых тел близки бесконечные семейства призм и антипризм (последние также называют скошенными призмами).

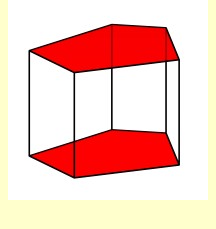
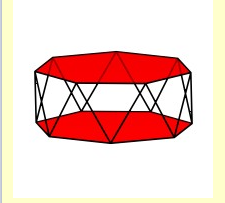
Бесконечные семейства призм и антипризм, вообще говоря, можно включить в множество архимедовых тел, но исторически по соображениям симметрии их выделяют в отдельные группы. Так же, как и архимедовы тела, выпуклые призмы и антипризмы — это выпуклые однородные многогранники, имеющие граниями несколько различных выпуклых многоугольников.